
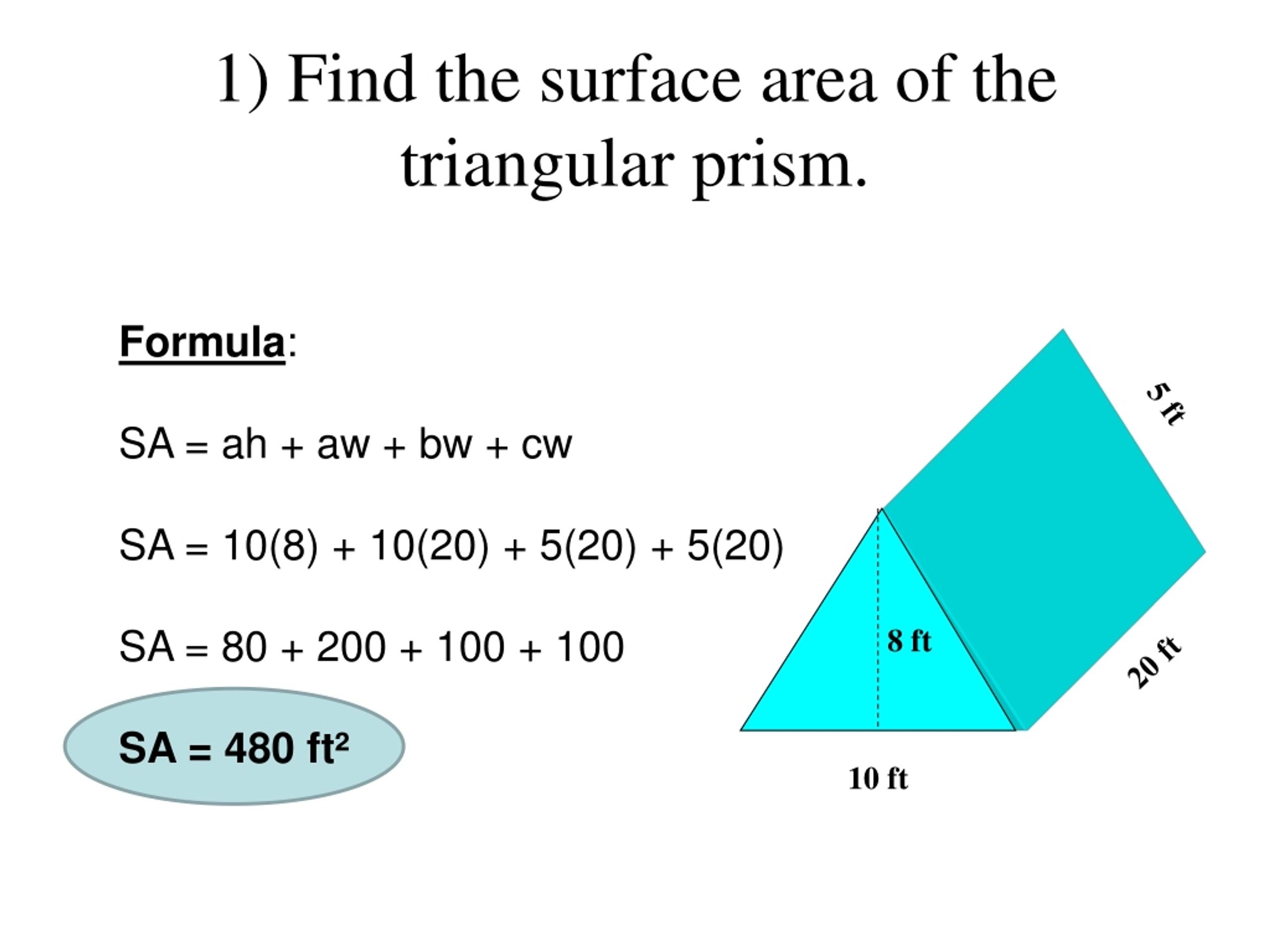
Now we don’t have any units for this shape, so we could say that it’s an area of 408 square units because an area should be squared. Lateral Surface Area of a Triangular Prism Formula. Adding these numbers together, we get 408. And then we have six times 15, which is 90, and then eight times 15, which is 120, and then 10 times 15, which is 150. So we’ll repeat that process again for the second triangle. One-half times eight times six, well one-half times eight is four, and four times six is 24. So we need to take six times 15 for the pink rectangle, eight times 15 for the green rectangle, and 10 times 15 for the blue rectangle. Now we have the rectangles, and the area of a rectangle is length times width. So we can either take that and multiply by two or write it twice since we have two triangles. And it’s important that we know that that’s a right angle in the corner of the triangle, because that let’s us know that the six is indeed perpendicular. So for the two rectangles, we have one-half times their base of eight times their perpendicular height, which is six. The area of a triangle is one-half times the base times the height. So if we find the area of each of these shapes and we add them together, we will have the surface area. So here we’ve drawn the net of the shape. We have the bottom rectangle, and keep in mind that these are not to scale, and then lastly the blue rectangle. So we have these two triangles, which are our bases we have the pink rectangle, found back here and we have this length as 15, because it matches this one.

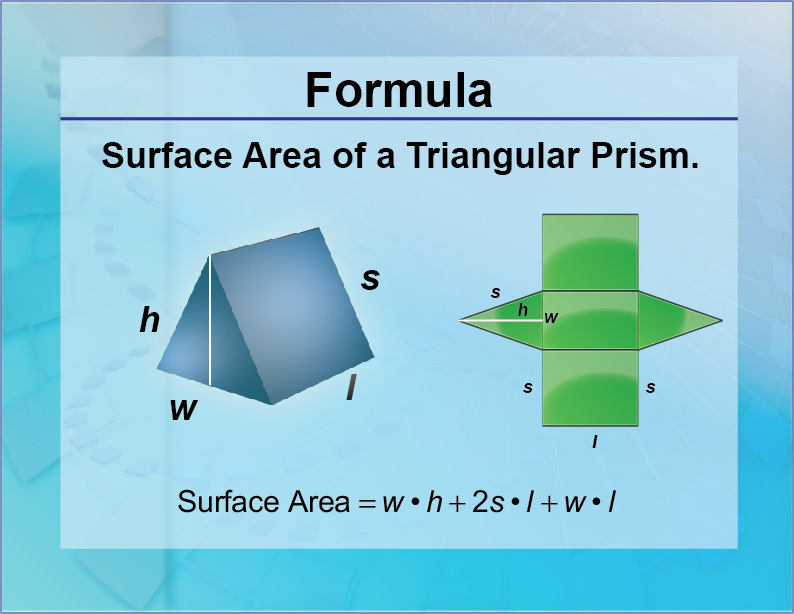
So our hint tells us to draw the net of this shape, which would be all of the faces laying flat so we can easily see them. So if we would like the surface area of this shape, we need to add the area of all of the faces together. That’s what makes up a prism: the two bases and then the rest are rectangles. And it’s a prism because the rest of the faces or the sides is what we can call them are rectangles. The bases, the parallel faces, are triangles. So we have- that this is a triangular prism. Hint: you can draw the net of the shape to help you. This gives us our simplified formula as A = bh + 3bL.Find the surface area of this triangular prism. 2.) We can use this to replace (s1 + s2 + s3) in the formula with 3b. Problem 2: If we are given a triangular prism that has a base formed by an equilateral triangle, how can we simplify the surface area formula before solving it? Solution: 1.) Since an equilateral triangle is made of three equivalent side lengths, we know that our s1 = s2 = s3. A = 123.31 4.) The surface area of the right-angled triangular prism is 123.31. 3.) Now let’s plug our known values into the surface area formula. Using the Pythagorean theorem, we get: (s3) 2 = 4 2 + 7 2 s3 = 8.062. 2.) We are still missing s3, which is the hypotenuse of the right triangle. These will also be our first two sides, so s1 = 4 and s2 = 7.
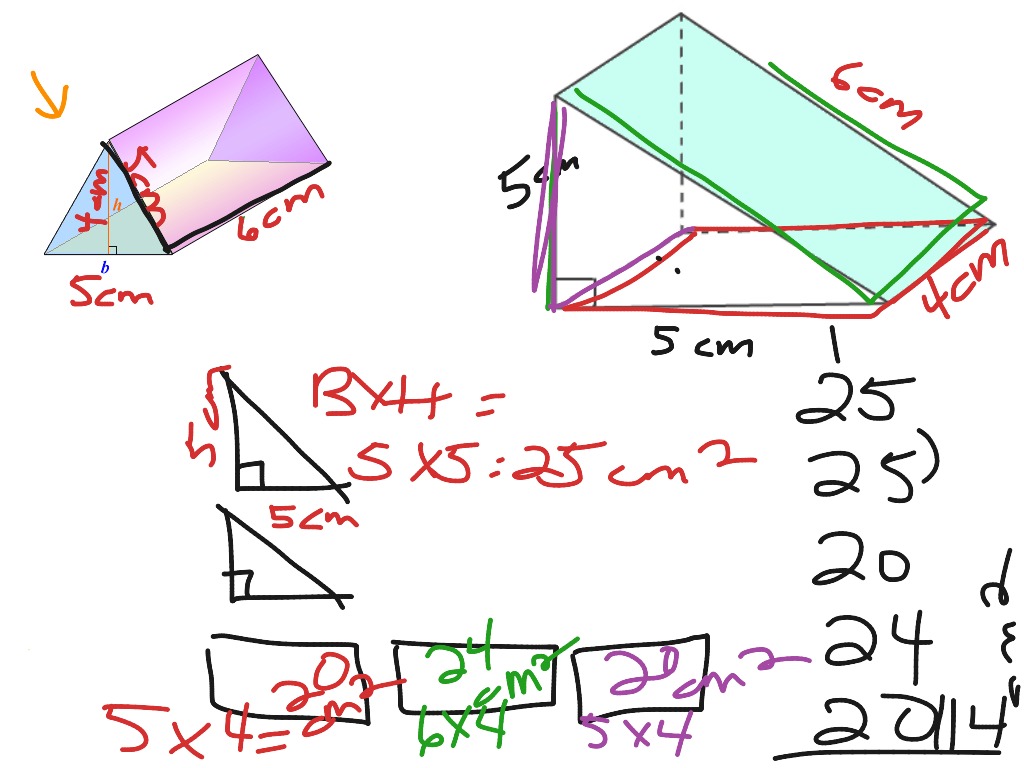
Solution: 1.) Since the base of the prism is formed by a right triangle and we know the leg lengths of the triangle, we can use the legs as the base and height. Find the surface area of the triangular prism.
The lateral faces of the prism are formed by a rectangle with a length of 5. Problem 1: The bases of a triangular prism are formed by a right triangle with leg lengths of 4 and 7.


 0 kommentar(er)
0 kommentar(er)
